ワープロ専用機を再現してみる
ワープロ専用機って
2000年をまたぐ頃に主要電機メーカーが製造中止を発表した文書作成することに特化した専用のコンピュータ。コンピュータと言っても電源入れるとすぐにキーボードからかな漢字変換を用いて日本語を入力し、すぐに印刷して使える。これに複写機があれば簡単に文書が配布できるものだった。
コンピュータの知識不要。表示は日本語と至れり尽くせり。Windows95の登場までは文書作成の中心だった。ワープロ専用機がPCに置き換わってワープロ専用機メーカーがWindows用ソフトを出してはいたがMS-Wordには勝てなかった。
再現した理由
再現した理由。
その1
今でもワープロ専用機でないと使えない人々がニコイチ修理依頼、ニコイチ販売業者かえら購入する形態が残っている。2010年までは稼働していた中古などを整備してもできた。2020年代も後半に入りワープロ専用機に中古販売の業者広告も減ったように感じる。あと10年すれば存在自体が20世紀の遺物として資料に残るだけになるだろう。
その2
8ビットパソコンなどは根強いファンがいて、資料収集や技術の伝承などが行われている。ワープロ専用機といえば散逸状態と言っていいほどである。ワープロ専用機のイメージはPC全盛になったころはさげすまれていたように感じる。体系的に収集、記録している方もいるとは思えても、8ビットPCのように熱心な方々は少ないと思える。
ゆえにワープロ専用機がどのように操作したのか動いたのかのエミュレータも存在は皆無に近いとおもわれる。ならばと思って再現した。
再現範囲
作成
ブラウザのみで動くJavascriptにてGeminiに指示を出して生成している。生成AIはある程度ワープロ専用機の情報が学習されている。
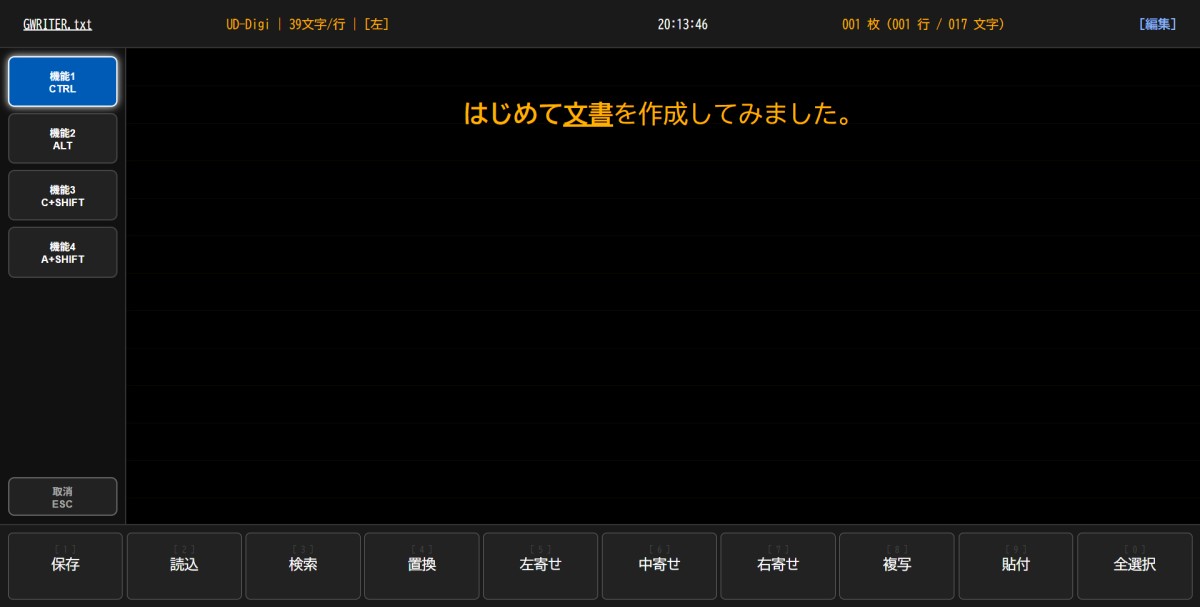
機能キー
ワープロ専用機は機能キー(2つが中心)+数字キーにて本体に刻印されている機能が実行できた。機能1キーを押しながら5とかという使い方である。ファンクションキーと機能キー併用という機種も1990年代ごろから登場した。
キーボードのCTRLを押すと、機能1 シフト押しながら押すと機能3。ALTは機能2、シフトを押すと機能4としてわかりやすくしている。きのうの選択はキーボード上部の1~0を選択する。マウスで操作も可能にしている。
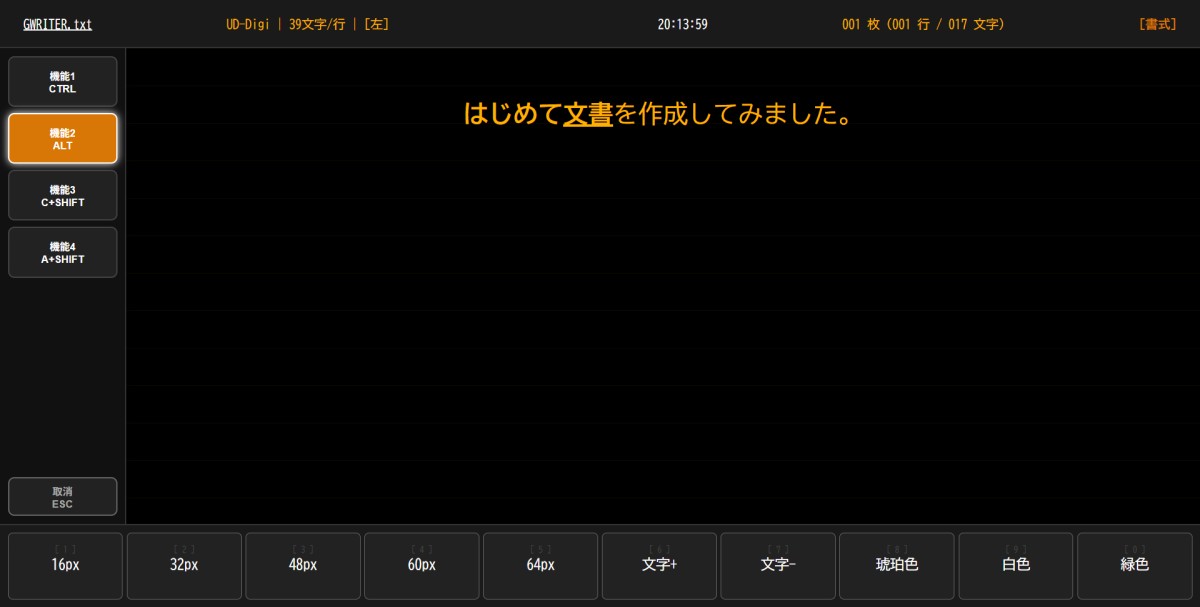
書式設定
本来なら生成AIGeminiに書式設定画面を再現したかったが、AIに取って要求が多すぎたのか1つ機能を入れるとこれまでの機能を動かなくしてしまうから文字サイズを変えるという方式に変えた。
印刷
OS(この場合はWindows)の印刷画面を呼び出す方式にしている。今のところA4横書き、縦長のみ。
保存呼び出し
保存はブラウザからダウンロード。呼び出しは基本ダウンロードフォルダから読み込めるようにしている。
マウス
ブラウザを操作するから必須。文書作成中はキーボードのみでも運用できるようにしている。
文書記憶
ブラウザを閉じても文書はブラウザ内に一時記憶できるようにしてすぐに始められるようにしている。
その他
CTRL+X,C,Vなどはそのまま使える。通常のテキストメモとして活用できる。PCもフォントを呼び出して変えることができる。
効用
ブラウザがあれば動くようにしているのでPCがあれば即ワープロ専用機の体験ができる。ニコイチ修理を探さずに今お使いのPCを即席ワープロ専用機にできる。
試用・免責
https://nanzo.net/GWriter/
にアクセスすると使える。試してほしい。不具合が起きた場合は報告してほしい。なお、このWebアプリはあくまでも昭和・平成を懐かしむ体験ができるというもの。実用には向いていない。重要な文書を作っていたら消えた責任を取れと言われても対処はできない。その点を了解して使ってほしい。




 写真右のSHARP EL-501Tが現行モデルとして入手できる。1,000円前後。手のひらサイズ。軽くキーも反応が良い。
写真右のSHARP EL-501Tが現行モデルとして入手できる。1,000円前後。手のひらサイズ。軽くキーも反応が良い。